我们需要将自己看做语言的设计者,而不只是由他人设计的语言用户。
计算机程序的构造和解释
递归
函数递归
一个将英文单词转换为它的 Pig Latin 等价形式的例子:
1
2
3
4
5
6
7
8
| def pig_latin(w):
"""Return the Pig Latin equivalent of English word w."""
if starts_with_a_vowel(w):
return w + 'ay'
return pig_latin(w[1:] + w[0])
def starts_with_a_vowel(w):
"""Return whether w begins with a vowel."""
return w[0].lower() in 'aeiou'
|
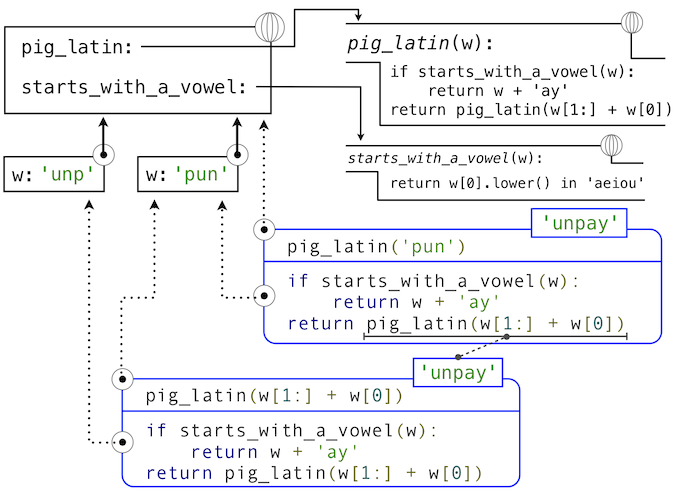
以上,将会产生函数的递归调用pig_latin->pig_latin, 我们可以看下面的环境图示,每次递归调用都将产生新的递归环境,也就是产生新的内存消耗。这就至少说明,递归是有最大深度限制的,最大深度取决于每次递归的环境大小和总内存大小之间的关系。不过, 按照我的理解,如Python这种语言会在解释器层面限制最大递归深度。

从上图我们也可以看到一些别的东西, 如变量引用。两次递归都使用了同一个pun,而不是会复制一份。
递归也像一个数学归纳的过程,以下是计算阶乘的递归函数的一段说明:
我们不应该关心fact(n-1)如何在fact的函数体中实现;我们只需要相信它计算了n-1的阶乘。将递归调用看做函数抽象叫做递归的“信仰飞跃”(leap of faith)。
这看起来就是数学归纳的过程,所以我想,递归和动态规划应该是同一类问题吧? 动态规划也是一个数学归纳过程。 这两种编程方法应该是可以互相转换的。下面有一个计算斐波那契数列的例子,使用了递归实现,但是也有状态转移方程,也存储了计算的中间结果。
一个使用记忆函数计算斐波那契数列的例子, 实现方式值得学习:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| def fib(n):
if n == 1:
return 0
if n == 2:
return 1
return fib(n-2) + fib(n-1)
def memo(f):
"""Return a memoized version of single-argument function f."""
cache = {}
def memoized(n):
if n not in cache:
cache[n] = f(n)
return cache[n]
return memoized
fib = memo(fib)
fib(40)
|
状态转移方程在fib函数中有体现,中间结果的保存过程则体现在memo函数中。初看这个实现方式时,着实令我眼前一新的感觉,代码很现代,值得学习。
数据递归
数据递归在数据抽象这一章出现了很多。我对数据递归的理解如下:
- 可以迭代
- 子集和全集结构相似
所以,以下数据结构一般都可以是递归结构:
- 列表(list,tuple,set,array等等)
- 树
组合语言解释器
参考和补充原文,实现一个计算器语言:
- 支持四个运算符:add,sub,mul,div
- 计算器运算符可以接受任意数量参数
- 运算符可以组合
如:
1
2
| calc> mul(add(2,3), sub(10,2), div(2,add(3,3,3)))
8.88888888888889
|
实现如下, 源码在github。
抽象表达式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class Exp():
"""
表达式抽象, 操作符和操作数
通过cal_apply调用, cal_apply(operator, operands)
"""
def __init__(self, operator, operands):
self.operator = operator
self.operands = operands
def __repr__(self):
return 'Exp({0}, {1})'.format(repr(self.operator), repr(self.operands))
def __str__(self):
operand_strs = ', '.join(map(str, self.operands))
return '{0}({1})'.format(self.operator, operand_strs)
|
执行运算符
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| def cal_apply(op, args):
"""
正式计算, 但是没有递归, 所以需要有别的模块解决递归计算问题
cal_apply(operator, operands)
"""
if op in ("add", "+"):
return sum(args)
if op in ("sub", "-"):
if len(args) == 0:
raise TypeError("{} require 1 argument at least".format(op))
elif len(args) == 1:
return -args[0]
else:
return sum(args[:1] + [-arg for arg in args[1:]])
if op in ("mul", "*"):
return reduce(mul, args, 1)
if op in ("div", "/"):
if len(args) != 2:
raise TypeError("{} require 2 argument".format(op))
else:
return args[0] / args[1]
|
解析表达式
1
2
3
4
5
6
7
8
9
10
| def calc_parse(line):
"""
解析表达式, 返回值是Exp
先将表达式的各个元素拆开, 再组合为Exp格式
"""
tokens = tokenize(line)
expression_tree = analyze(tokens)
if len(tokens) > 0:
raise SyntaxError('Extra token(s): ' + ' '.join(tokens))
return expression_tree
|
词法分析
1
2
3
4
5
6
| def tokenize(line):
"""
拆分表示各个元素
"""
spaced = line.replace('(', ' ( ').replace(')', ' ) ').replace(',', ' , ')
return spaced.split()
|
语法分析
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| known_operators = ['add', 'sub', 'mul', 'div', '+', '-', '*', '/']
def analyze(tokens):
"""
表达式元素组合,形成操作树
"""
assert_non_empty(tokens)
# 数字或者操作符
token = analyze_token(tokens.pop(0))
# 如果是数字,直接放回就好了,继续求下一个,因为数字是自求解的,本身就是解
if type(token) in (int, float):
return token
# 如果是操作符,则需要组合为Exp表达式
if token in known_operators:
# 当前是操作符, 则需要检查后面有没有操作数
# 计算器的操作符后面是有操作数的
# 操作数递归组合即可
if len(tokens) == 0 or tokens.pop(0) != '(':
raise SyntaxError('expected ( after ' + token)
return Exp(token, analyze_operands(tokens))
else:
raise SyntaxError('unexpected ' + token)
def analyze_operands(tokens):
"""
生成操作数
"""
assert_non_empty(tokens)
operands = []
# 直到闭括号
while tokens[0] != ')':
if operands and tokens.pop(0) != ',':
raise SyntaxError('expected ,')
operands.append(analyze(tokens))
assert_non_empty(tokens)
tokens.pop(0) # 移除闭括号‘)’
return operands
def assert_non_empty(tokens):
"""Raise an exception if tokens is empty."""
if len(tokens) == 0:
raise SyntaxError('unexpected end of line')
def analyze_token(token):
"""Return the value of token if it can be analyzed as a number, or token."""
try:
return int(token)
except (TypeError, ValueError):
try:
return float(token)
except (TypeError, ValueError):
# 如果不是数字, 则可能是表达式, 先直接返回
return token
|
递归表达式
将表达式递归成执行器可以理解的。
1
2
3
4
5
6
7
8
| def calc_eval(expression):
"""
表达式递归求解, 从里到外依次求解
"""
expression.operands = [calc_eval(operand) if type(operand) == type(
expression) else operand for operand in expression.operands]
cal_apply_result = cal_apply(expression.operator, expression.operands)
return cal_apply_result
|
读取输入
1
2
3
4
5
6
7
8
9
10
11
| def read_eval_print_loop():
"""Run a read-eval-print loop for calculator."""
while True:
try:
expression_tree = calc_parse(input('calc> '))
print(calc_eval(expression_tree))
except (SyntaxError, TypeError, ZeroDivisionError) as err:
print(type(err).__name__ + ':', err)
except (KeyboardInterrupt, EOFError):
print('Calculation completed.')
return
|